Understanding mathematical concepts follows a natural progression throughout a child’s educational journey. Parents often wonder when their children will encounter more advanced topics like square roots. According to educational resources from Study Watches, square root concepts typically emerge during middle school years, though the groundwork begins much earlier through basic multiplication and division skills.
The journey toward understanding square roots starts with fundamental arithmetic operations. Children first master addition and subtraction in elementary grades, then progress to multiplication tables and division facts. These building blocks create the foundation necessary for comprehending inverse operations, which square roots represent.
Most students encounter formal square root instruction around seventh or eighth grade, typically between ages 12 and 14. However, the specific timing depends on individual school districts and curriculum standards. To learn more about grade-level expectations, you can explore detailed information about what grade do you learn square root concepts in various educational systems.
Early Mathematical Foundation Building
Before diving into square roots, children need solid arithmetic skills. Elementary students spend considerable time mastering basic operations through repeated practice and memorization. This foundational work typically occurs between kindergarten and fifth grade.
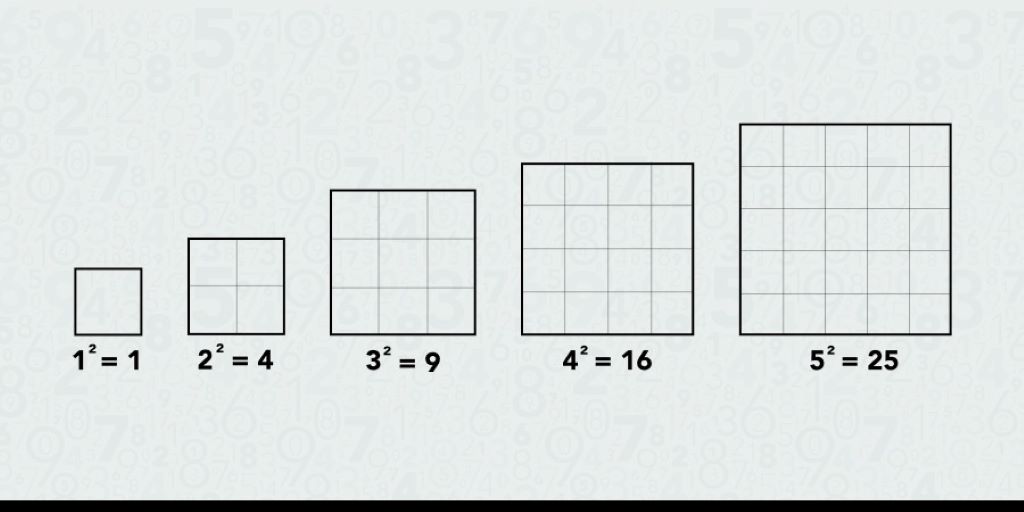
During these early years, teachers introduce concepts like perfect squares through multiplication tables. Students learn that 3 × 3 equals 9, 4 × 4 equals 16, and 5 × 5 equals 25. While they may not immediately connect these to square roots, this knowledge becomes crucial later.
Pattern recognition also plays an important role during elementary years. Children observe relationships between numbers and begin understanding how mathematical operations work together. These skills prepare them for more complex concepts they will encounter in middle school.
Introduction to Square Root Concepts
Middle school marks the formal introduction to square root notation and rules. Sixth-grade students often encounter basic square root problems involving perfect squares. Teachers present these concepts gradually, starting with simple examples before advancing to more complex scenarios.
The square root symbol (√) gets introduced alongside explanations of what it represents. Students learn that finding a square root means determining which number, when multiplied by itself, produces the given value. For example, the square root of 16 is 4 because 4 × 4 equals 16.
Interactive activities help students grasp these concepts more effectively. Teachers might use visual aids, manipulatives, or technology to demonstrate how square roots work. Games and puzzles make learning more engaging while reinforcing important mathematical principles.
Grade-Level Progression and Standards
Educational standards vary between states and countries, but general patterns emerge regarding square root instruction. Most curriculum guides place initial square root concepts in seventh grade, with deeper exploration continuing through eighth grade and beyond.
Seventh-grade students typically learn to identify perfect square roots and understand the relationship between squaring and taking square roots. They practice calculating simple square roots mentally and begin using calculator tools for more complex problems.
Eighth-grade instruction expands to include estimating square roots of non-perfect squares and applying these skills to geometry problems. Students might calculate the length of triangle sides or determine distances using the Pythagorean theorem.
High school courses build upon these foundations with more advanced applications. Algebra students work with square root expressions in equations, while geometry students apply square root calculations to various spatial problems.
Common Challenges Students Face
Learning square roots presents unique difficulties for many students. The concept of inverse operations can be confusing initially, especially for children who struggle with abstract thinking. Unlike addition or multiplication, square roots don’t follow immediately obvious patterns.
Memorizing perfect squares requires significant practice and repetition. Students often find it challenging to recall that 144 is 12 squared or that 169 equals 13 squared. Regular review and creative memory techniques help overcome these obstacles.
Calculator dependency poses another common challenge. While technology assists with complex calculations, students need to develop mental math skills for simple square roots. Teachers emphasize the importance of knowing perfect squares without relying on electronic aids.
Effective Teaching Strategies
Successful square root instruction combines multiple teaching approaches. Visual learners benefit from geometric representations showing how square roots relate to actual square shapes. Teachers might use graph paper to create squares with different areas, helping students visualize the connection.
Hands-on activities engage kinesthetic learners effectively. Building physical squares using blocks or tiles demonstrates the concept tangibly. Students can manipulate materials to discover patterns and relationships independently.
Technology integration enhances modern square root instruction. Interactive software allows students to explore square root concepts dynamically. Online games and apps provide additional practice opportunities outside traditional classroom settings.
Connecting square roots to real-world applications increases student engagement. Examples might include calculating distances, determining screen sizes, or solving construction problems. These practical applications help students understand why square root skills matter beyond academic settings.
Supporting Learning at Home
Parents play crucial roles in reinforcing square root concepts outside school. Simple activities can supplement classroom instruction effectively. Family math games incorporating perfect squares make practice enjoyable while strengthening recall abilities.
Creating flashcards for perfect squares helps with memorization. Parents can quiz children regularly, gradually increasing difficulty levels. Celebrating progress maintains motivation and builds confidence in mathematical abilities.
Connecting math to daily activities reinforces learning naturally. Measuring rooms, calculating areas, or working on home improvement projects provide authentic square root applications. These experiences demonstrate practical value while strengthening conceptual understanding.
Preparing for Advanced Mathematics
Strong square root foundations prepare students for advanced mathematical coursework. Algebra heavily relies on square root manipulation and simplification skills. Students who master these concepts early experience greater success in higher-level mathematics.
Geometry applications become more sophisticated as students progress. Advanced problems involving the Pythagorean theorem, distance formulas, and trigonometric functions all require solid square root abilities. Early mastery prevents future struggles with complex applications.
Standardized testing includes square root problems at various difficulty levels. Students benefit from consistent practice and review throughout their mathematical education. Strong foundations lead to improved test performance and increased educational opportunities.
Technology and Modern Learning
Digital tools transform how students learn square root concepts today. Interactive websites provide immediate feedback and personalized instruction. Students can progress at individual paces while receiving targeted support for specific challenges.
Calculator skills require careful balance with mental math abilities. Students need to understand when technology helps and when manual calculation is appropriate. Teachers emphasize developing both skill sets for comprehensive mathematical competence.
Online resources supplement traditional textbooks effectively. Video tutorials, practice websites, and educational apps provide additional learning opportunities. These tools cater to different learning styles and offer flexible scheduling options.
Assessment and Progress Monitoring
Regular assessment helps teachers identify students needing additional support. Formative assessments during instruction reveal misunderstandings before they become entrenched. Quick check-ins and exit tickets provide valuable feedback about student comprehension.
Summative assessments measure overall progress toward learning objectives. These evaluations help determine whether students are ready for more advanced concepts or need additional reinforcement with current material.
Individual progress monitoring ensures no student falls behind. Teachers track skill development over time, adjusting instruction based on individual needs. This personalized approach maximizes learning outcomes for all students.
Conclusion
Square root learning typically begins formally in middle school, around seventh or eighth grade, though foundational skills develop much earlier. The progression from basic arithmetic through perfect squares to complex applications requires patience, practice, and effective instruction. Students who master these concepts early position themselves for success in advanced mathematics courses.
Understanding when children learn square roots helps parents and educators provide appropriate support at each stage. With proper foundation building, engaging instruction, and consistent practice, students can develop strong square root skills that serve them throughout their mathematical education and beyond.
Frequently Asked Questions
What grade do students typically learn square roots? Most students begin learning square root concepts in seventh or eighth grade, usually between ages 12-14, though this varies by curriculum and individual readiness.
Do students need to memorize all perfect squares? Students should memorize perfect squares from 1-144 (1² through 12²) as these appear most frequently in middle and high school mathematics problems.
How can parents help children learn square roots at home? Parents can use flashcards for perfect squares, incorporate math into daily activities like measuring, and play mathematical games that reinforce square root concepts.
Why do some students find square roots difficult? Square roots involve inverse operations and abstract thinking, which can be challenging. The concept requires understanding relationships between numbers rather than simple computation.
When do students use calculators for square root problems? Students should master perfect squares mentally first, then learn calculator skills for non-perfect squares and complex applications in advanced coursework.
Read More:
How to Choose the Best Administrative Assistant Education





